Kérdésjegyzék
(Checklist)
|
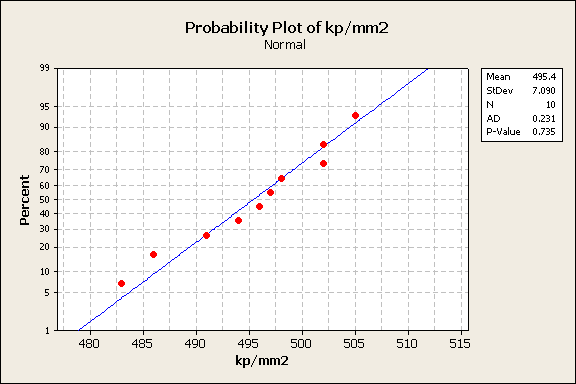
Az adatok ésszerűen normális eloszlásúak? (próba robosztus a nem normális adatokra)
Are the data reasonably normal? (test is very robust to non-normal data)
|
|
|
A mérőrendszer validált?
Has the measurement system been validated?
|
|
|
A mintanagyság követelményei meghatározottak?
Have you determined the sample size requirements?
|
|
What is the recommended sample size?
|
| Minitab: Stat > Power and Sample Size > 1-Sample t | |
|
Mekkora a legkisebb változás a várható értékben, melyet ki akarunk mutatni?
What is the smallest change in the mean you want to detect?
|
|
|
Mekkora a feltételezett szórás értéke?
What is the assumed value of the standard deviation?
|
|
|
Mekkora a próba megkívánt ereje? (általában 80%)
What is the desired power for the test? (usually, 80%)
|
|
|
Mekkora a próba aktuális ereje az ajánlott mintanagyság esetén?
What is the actual power for the recommended sample size?
|
|
|
Ha nem használjuk az ajánlott mintanagyságot, akkor mekkora a legkisebb változás a várható értékben, melyet észlelni tudunk, feltételezve a próba 80%-os erejét és az aktuális mintanagyságot?
If you are not using the recommended sample size, what is the smallest change in the mean that you can detect, assuming power of 80% and your actual sample size?
|
|
Kimenet
(Output)
| p-value: |
Elemzések (t-próba eredménye,
próba ereje és mintanagyság, stb.)
Session (output from t Test, output from Power and Sample Size, etc):
Descriptive Statistics: kp/mm2
Variable N N* Mean SE Mean StDev Minimum Q1 Median Q3 Maximum
kp/mm2 10 0 495.40 2.24 7.09 483.00 489.75 496.50 502.00 505.00
Variable N N* Mean SE Mean StDev Minimum Q1 Median Q3 Maximum
kp/mm2 10 0 495.40 2.24 7.09 483.00 489.75 496.50 502.00 505.00
One−Sample T: kp/mm2
Test of mu = 500 vs < 500
95% Upper
Variable N Mean StDev SE Mean Bound T P
kp/mm2 10 495.40 7.09 2.24 499.51 −2.05 0.035
Test of mu = 500 vs < 500
95% Upper
Variable N Mean StDev SE Mean Bound T P
kp/mm2 10 495.40 7.09 2.24 499.51 −2.05 0.035
Power and Sample Size
1−Sample t Test
Testing mean = null (versus < null)
Calculating power for mean = null + difference
Alpha = 0.05 Assumed standard deviation = 7.09
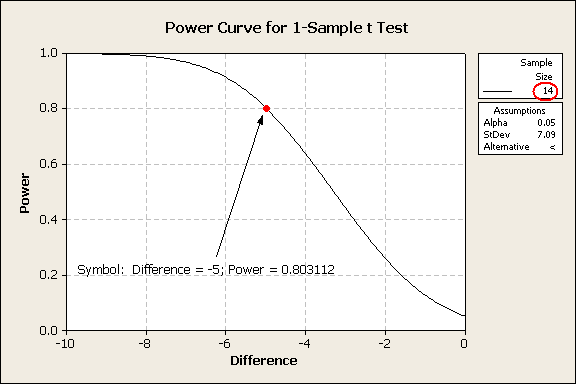
Sample Target
Difference Size Power Actual Power
−5 14 0.8 0.803112
1−Sample t Test
Testing mean = null (versus < null)
Calculating power for mean = null + difference
Alpha = 0.05 Assumed standard deviation = 7.09
Sample Target
Difference Size Power Actual Power
−5 14 0.8 0.803112
Power and Sample Size
1−Sample t Test
Testing mean = null (versus < null)
Calculating power for mean = null + difference
Alpha = 0.05 Assumed standard deviation = 7.09
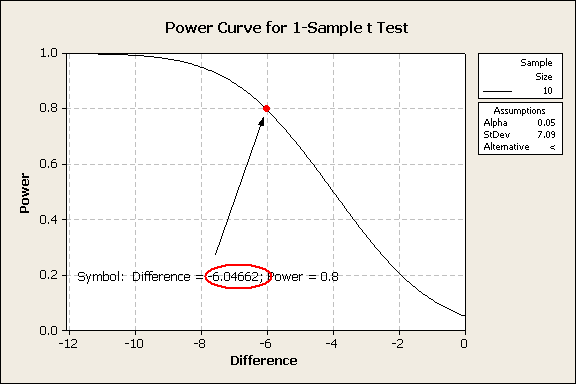
Sample
Size Power Difference
10 0.8 −6.04662
1−Sample t Test
Testing mean = null (versus < null)
Calculating power for mean = null + difference
Alpha = 0.05 Assumed standard deviation = 7.09
Sample
Size Power Difference
10 0.8 −6.04662
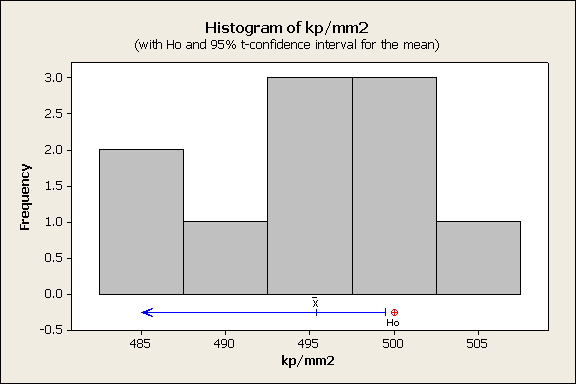
Ábrák (opcionális, pl. Hisztorgram vagy Egyedi értékek ábra, stb.)
Graphical (optional, may include a Histogram or Individual Value Plot, etc.):